Getting Started with OneMax

This tutorial explains how to implement custom representations, including: (a) one Individual, (b) one Variator, and (c) one Evaluator.

Representation

To begin, implement a custom representation.

All custom representations must (a) derive evokit.core.population.Individual, (b) store the genotype in Individual.genome, and (c) override Individual.copy.

The implementation decides how to create new individuals. Here, the class BinaryString implements a factory method BinaryString.random, which creates a uniformly random bit string of a certain length.

[23]:

from __future__ import annotations
from typing import List, Self

from random import getrandbits
from evokit.core.population import Individual

class BinaryString(Individual[List[int]]):
    def __init__(self, value: List[int]) -> None:
        self.genome: List[int] = value

    @staticmethod
    def random(len: int) -> BinaryString:
        return BinaryString(
            (len * [0] +
                [int(digit) for digit in bin(getrandbits(len))[2:]])[-len:]
        )

    def copy(self: Self) -> Self:
        return type(self)(self.genome.copy())

    def __str__(self: Self) -> str:
        return str(self.genome)

Variator

Implement a custom variator of BinaryString. All variators must derive evokit.core.variator.Variator and override Variator.vary.

This variator has .arity=1, means that it only takes one parent. Consequently, its .vary method can expect a tuple of size 1.

The implementation of .vary returns a tuple of size 1. To inform the user of this behaviour, the implementation should set .coarity=2.

[24]:

from random import random
from typing import Sequence, Tuple

from evokit.core.variator import Variator

class RandomBitMutator(Variator[BinaryString]):
    def __init__(self, mutation_rate: float):
        self.arity = 1
        self.coarity = 2
        if (mutation_rate < 0 or mutation_rate > 1):
            raise ValueError(f"Mutation rate must be within {0} and {1}."
                             f"Got: {mutation_rate}")
        self.mutation_rate = mutation_rate

    def vary(self, parents: Sequence[BinaryString]) -> Tuple[BinaryString, ...]:
        offspring = parents[0].copy()

        for i in range(0, len(offspring.genome)):
            if (random() < self.mutation_rate):
                offspring.genome[i] = 1 if offspring.genome[i] == 0 else 1

        return (offspring,)

Evaluator

Then, implement a custom evaluator of BinaryString.

All custom evaluators must derive evokit.core.evaluator.Evaluator and override Evaluator.evaluate. Here, BitDistanceEvaluator sums all bits in the genotype of a BinaryString.

[25]:

from evokit.core.evaluator import Evaluator
from typing import override

class BitDistanceEvaluator(Evaluator[BinaryString]):
    @override
    def evaluate(self, s1: BinaryString) -> float:
        return sum(s1.genome)

Put Everything Together

Create and run an evolutionary algorithm using components that have already been defined.

Since selectors and the overall algorithm do not depend on representations, the framework comes with generic ones thatare compatible with all representations.

Import a selector and an algorithm from evokit.core.selector and evokit.core.algorithm respectively:

Together, Elitist and SimpleSelector form an elitist selector that always selects for highest-fitness individuals.
The SimpleLinearController applies operators in the following order:
1. evaluate for selection
2. selection
3. update population
4. vary parents
5. update population

[26]:

from evokit.core.selector import Elitist, SimpleSelector

from evokit.core.algorithm import SimpleLinearAlgorithm

Initialise Population

Create a number of BinaryString instances, then store them in a Population.

[27]:

from evokit.core.population import Population

BINSTRING_LENGTH: int = 1000
POPULATION_SIZE: int = 20
GENERATION_COUNT: int = 100
init_pop = Population[BinaryString]()

for i in range(0, POPULATION_SIZE):
    init_pop.append(BinaryString.random(BINSTRING_LENGTH))

Define the Algorithm

Initialise operators, then run the algorithm with these operators.

[28]:

ctrl: SimpleLinearAlgorithm = SimpleLinearAlgorithm(
    population=init_pop,
    variator=RandomBitMutator(0.1),
    selector=Elitist(SimpleSelector[BinaryString](POPULATION_SIZE)),
    evaluator = BitDistanceEvaluator()
)

Run the Algorithm

Run the algorithm, then retain the best individual of each generation. Remember to call copy, so that subsequent modifications on the individual do not affect the retained copy.

[29]:

bests = []

for _ in range(GENERATION_COUNT):
    ctrl.step()
    bests.append(ctrl.population[0])

Analyse Results

Print best individuals of the first and last generations. Note the that the latter has significantly higher fitness.

[30]:

print(f"Best individual of the first generation is {bests[0]}")
print(f"    with fitness {sum(bests[0].genome)}")
print(f"Best individual of the last generation is {bests[-1]}")
print(f"    with fitness {sum(bests[-1].genome)}")

Best individual of the first generation is [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0]
    with fitness 579
Best individual of the last generation is [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
    with fitness 1000

[31]:

from matplotlib import pyplot as plt
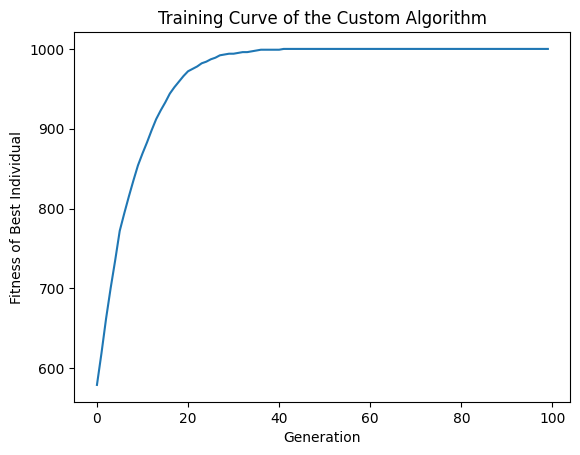
plt.title('Training Curve of the Custom Algorithm')
plt.xlabel('Generation')
plt.ylabel('Fitness of Best Individual')
plt.plot([i for i in range(len(bests))], [sum(x.genome) for x in bests])
plt.show()

../../_images/guides_examples_onemax_17_0.png